The Brookbush Institute Publishes a NEW Glossary Term: 'Null-hypothesis'

The Brookbush Institute continues to enhance education with new courses, a modern glossary, an AI Tutor, and a client program generator.

NEW YORK, NY, UNITED STATES, August 21, 2025 /EINPresswire.com/ -- - Excerpt from Glossary Term: Null Hypothesis
- Additional Glossary Term: Evidence-based Practice
- Related Certification: Human Movement Specialist (HMS) Certification

DEFINITION:
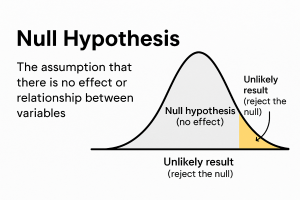
Null Hypothesis: The null hypothesis is a foundational concept in statistical hypothesis testing. It represents the assumption of no effect, no difference, or no relationship between variables. It serves as a starting point or baseline for statistical comparison. Research is conducted with the aim of either refuting (rejecting) or failing to refute the null hypothesis. This is determined based on whether the observed data demonstrates a significant difference from "no effect."

Clarification: The null hypothesis is not the same as an opposing position or alternative theory. It is specifically the assumption that any observed effect is due to random variation or chance. It is the "no effect" hypothesis, not "the opposite effect" hypothesis.

Purpose and Function: The null hypothesis provides a statistical anchor. It provides the default assumption (no relationship) that can be tested with data. For example, in a study comparing two treatments, the null hypothesis would state that there is no difference in their effects.

Once data is collected, statistical tests determine the probability of observing the study's findings assuming the null hypothesis is true. If this probability (p-value) is sufficiently small (e.g., p < 0.05), the null hypothesis is rejected. The null hypothesis is rejected because the difference in the data was so "extreme" that it would be highly unlikely to occur by chance if the intervention had actually had no effect.

HOW TO WRITE A NULL HYPOTHESIS

To write a null hypothesis, begin by formulating a research question. Then rephrase that question in a way that assumes no relationship between the variables of interest. In other words, the null hypothesis is always framed as if the treatment, condition, or exposure has no effect on the outcome. The wording should be precise, measurable, and testable so that statistical analysis can evaluate whether the null hypothesis can be rejected.

A null hypothesis is often written as H₀ and paired with an alternative hypothesis (H₁) that predicts a relationship or effect. Importantly, rejecting the null hypothesis does not prove the alternative hypothesis; it only indicates that the data are unlikely if the null hypothesis were true.

APPLIED EXAMPLE:
Research Question:
- Does eccentric hamstring training reduce the incidence of hamstring strains in collegiate soccer players?

Null Hypothesis (H₀):
- Eccentric hamstring training has no effect on the incidence of hamstring strains in collegiate soccer players.

Alternative Hypothesis (H₁):
- Eccentric hamstring training reduces the incidence of hamstring strains in collegiate soccer players.

WHY NOT TEST THE HYPOTHESIS DIRECTLY?
A hypothesis is a proposed explanation for a phenomenon that can be tested through research and experimentation. However, research can only demonstrate the likelihood of a relationship between variables and outcome measures. It does not prove why a relationship exists, nor does it determine the precise nature of that relationship. Theoretically, there may be an infinite number of contributing factors to why a relationship was observed (or not). Any hypothesis about why a relationship exists competes with all other plausible explanations, both known and unknown. In short, we cannot test the validity of a hypothesis against an infinite set of alternatives, but we can test the probability of a relationship between a variable and outcome measures.

When we test against the null hypothesis, we arrive at one of two outcomes:

We fail to reject the null hypothesis, implying that there is no relationship between the tested variables that cannot be explained by chance.
We reject the null hypothesis, indicating that a statistically significant difference from the null exists and that the observed relationship is unlikely to be due to random variation alone.

Determining causality requires methodically designed studies that aim to both demonstrate relationships and refute incorrect hypotheses. Note that a scientific approach, or evidence-based approach, to any topic involves accepting the hypothesis that is most consistently supported by evidence and has demonstrated the best reliability and accuracy for predicting outcomes in repeated experiments. For more reading, and a beautiful quote for a title, check out the article -

“Science: the slow march of accumulating evidence ” - Katherine Picho, Lauren A. Maggio, and Anthony R. Artino Jr.

FOR THE FULL TEXT AND SO MUCH MORE, CLICK ON THE LINK

Brent Brookbush
Brookbush Institute
Support@BrookbushInstitute.com
Visit us on social media:
LinkedIn
Instagram
Facebook
YouTube
TikTok
X
Other

Legal Disclaimer:

EIN Presswire provides this news content "as is" without warranty of any kind. We do not accept any responsibility or liability for the accuracy, content, images, videos, licenses, completeness, legality, or reliability of the information contained in this article. If you have any complaints or copyright issues related to this article, kindly contact the author above.